|
|
|
|
News The Project Technology RoboSpatium Contribute Subject index Download Responses Games Gadgets Contact <<< Hard or soft Eddy current >>> Electromagnetic inductionPrinciple of reversionAt the chapter magnetism we have learned that a moving charged particle creates a magnetic field. How to move charges, we have seen in front of that at the chapters about voltage and current. You can concentrate magnetic fields by arranging a wire like a coil. So you can create a magnetic field by simply connecting an inductor to a voltage source. Is the inverse process, thus creating voltage by a magnetic field, possible, too? Almost all physical laws are reversible like this. As an example I would like to mention the water actuated mill wheel: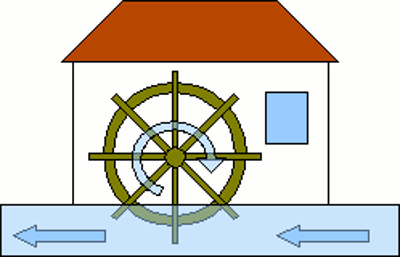
If water passes by a mill wheel, like drawn at the picture from the right to the left, the wheel starts rotating clockwise. The question is: "What happens, if the mill wheel is turned around anticlockwise by an engine?" Well, the mill wheel starts acting like a pump, moving the water to the right. 
I guess you have never seen a mill wheel pumping water uphill, but there is another use of this principle you might have seen in videos about the "good old times": the paddle wheel steamer. Law of inductionThe problem, how to create voltage by a coil and a magnet, kept many physicists busy, amongst them the English physicist Michael Faraday. He is generally credited with the discovery of the electromagnetic induction phenomenon. He figured out the following correlation:The electromotive force produced around a closed path is proportional to the rate of change of the magnetic flux through any surface bounded by that path. Expressed mathematically, we get the formula: Where is: ε - electromotive force (EMF) given in Volt, ΦB - magnetic flux given in Weber We already got to know the electromotive force as the difference between two electric potentials. The better known name is "voltage". The magnetic flux has not been mentioned directly, but we already know the magnetic flux density. Metaphorically spoken, the magnetic flux density matches the number of field lines running through an area being perpendicular to the field lines. The magnetic flux corresponds the "net number" of field lines running through a given area. Because of the fact that magnetic field lines point into a special direction, the net number is the number of field lines running in one direction minus the number of field lines running in the opposite direction. More strictly spoken, the flux density at each point of the area is added up, whereby just the fraction being perpendicular is included. In practiceTo generate voltage, we just have to alter the magnetic flux running through a wire being bound to a loop. Unfortunately the generated voltage is hard to measure inside a closed loop of a wire. So let's cut the loop and yet we are able to measure the voltage at the two ends of the wire. One more principle simplifies the measurement: If we take more than just one loop around (nearly) the same area, the total voltage increases, because it is the sum of the single voltages generated. We have recognized such an arrangement of many wire loops as a coil or an inductor. Using an inductor we get:Where is: N - Number of windings ε - electromotive force (EMF) given in Volt, ΦB - magnetic flux given in Weber By now we just have to alter the magnetic flux running through the loops to generate voltage. Let's take a permanent magnet and a coil with three windings: 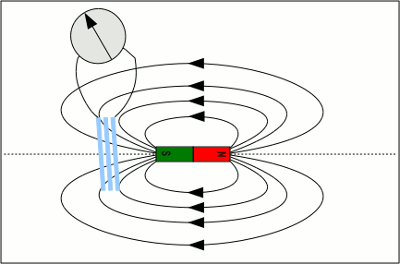
A coil with 3 windings, whose ends are connected to a voltmeter, is moved along a bar shaped permanent magnet. The magnetic poles are arranged at the axis of the coil. If the coil is moved with constant speed into the direction of the magnetic north pole, the number of magnetic field lines passing the coil and thereby the flux density is increasing. According to the law of electromagnetic induction, voltage is generated and the indicator of the voltmeter points to the right. Despite the constant speed of moving, the induced voltage increases, the closer the coil gets to the magnetic north pole. That is because of the fact that the number of field lines is increasing disproportionately high around the poles of the permanent magnet. Before reaching the north pole, the induced voltage reaches it's maximum. As soon as the magnet is diving into the coil, all field lines are running through the coil (inside of the magnet). The flux density doesn't increase any longer and for this reason the induced voltage becomes zero. As long as the poles of the magnet stick out of the coil, the magnetic flux remains unchanged. As soon as the coil leaves the magnet at the south pole, the number of field lines, passing the loops, is decreasing. Initially faster, because the field lines are running concentrated near the pole, afterwards some slower, because the density of field lines decreases disproportionately. The indicator of the voltmeter points to the opposite direction - from the highest negative value near the pole to zero at the end of the movement. The voltage generated by an alterning magnetic flux is called inductive or induced voltage. <<< Hard or soft Eddy current >>> News The Project Technology RoboSpatium Contribute Subject index Archives Download Responses Games Links Gadgets Contact Imprint |
|
|